二维前缀和，前缀和即当前元素与之前的元素之和，例如现有一个3行4列的矩阵

定义：本例中x和y从1开始，例如：(1, 1)的值为6，(2, 1)的值为7

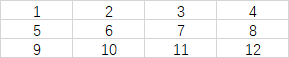
(1, 1)的前缀和即1 + 2 + 5 + 6 = 14

• 依次计算(0, 0)、(0, 1)、(1, 0)的前缀和

  • (0, 0)

  

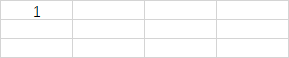
  • (0, 1)

    

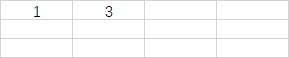
  • (1, 0)

    

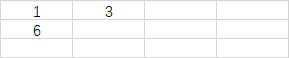
• 根据上面的结果，计算(1, 1)的前缀和

  

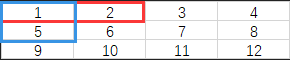
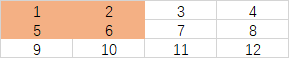
  (0, 1)的前缀和的值为3（红色矩形中的值相加）

  (1, 0)的前缀和的值为6（蓝色矩形中的值相加）

  计算(1，1)前缀和的值只需将红色矩形(0, 1)的前缀和值加上蓝色矩形(1, 0)的前缀和值，然后减去这两个矩形重叠的部分的前缀和的值（因为(0, 1)和(1, 0)的前缀和的包含了(0, 0)，也就是(0, 0)的前缀和值被多加了一遍，所以需要减去），再加上(1，1)处的值即可计算出(1, 1)的前缀和值

  3(红色矩形) + 6(蓝色矩形) - 1(重叠的部分) + 6(自身的值) = 14

  所以可以得出递推公式：DP(x, y) = DP(x - 1, y) + DP(x, y - 1) - DP(x - 1, y - 1) + M(x, y)

  #include <iostream>
  
  int M, N;
  int Martix[101][101];
  int DP[101][101];
  
  int main() {
  	std::cin >> M >> N;
  
  	for (int i = 1; i <= M; ++i) {
  		for (int j = 1; j <= N; ++j) {
  			std::cin >> Martix[i][j];
  		}
  	}
  
  	for (int i = 1; i <= M; ++i) {
  		for (int j = 1; j <= N; ++j) {
  			DP[i][j] = DP[i - 1][j] + DP[i][j - 1] - DP[i - 1][j - 1] + Martix[i][j];
  		}
  	}
  
  	printf("前缀和：\n");
  
  	for (int i = 1; i <= M; ++i) {
  		for (int j = 1; j <= N; ++j) {
  			printf("%d ", DP[i][j]);
  		}
  		printf("\n");
  	}
  
  	return 0;
  }
  
  /*
  input:
  3 4
  1 2 3 4
  5 6 7 8
  9 10 11 12
  
  output:
  1 3 6 10
  6 14 24 36
  15 33 54 78
  */