左倾红黑树实现及注释
左倾红黑树插入结果可视化:
插入顺序:6 7 1 5 3 4 2
put:6
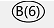
put:7

put:1
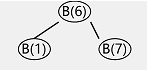
put:5
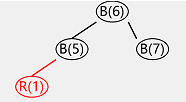
put:3
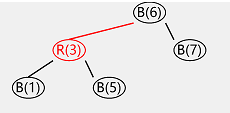
put:4
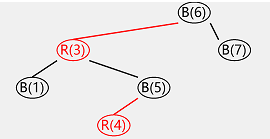
put:2
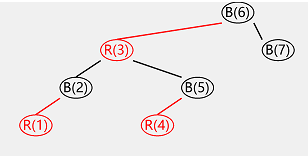
#include <iostream>
#include <cstdlib>
#include <ctime>
template<class _Key, class _Value>
class LLRBT
{
enum color_t { BLACK, RED };
struct Node
{
_Key key;
_Value value;
size_t count; //此节点所有孩子节点数+1
color_t color; //指向本节点的链接颜色
struct Node *left,
*right;
Node( const _Key & pKey,
const _Value & pValue,
color_t pColor = RED,
size_t pCount = 1,
struct Node * pLeft = nullptr,
struct Node * pRight = nullptr)
: key(pKey), value(pValue), count(pCount), color(pColor), left(pLeft), right(pRight) { }
};
//定义根节点
Node * root_ = nullptr;
void clear(Node * node)
{
if(node == nullptr) return;
clear(node->left);
clear(node->right);
delete node;
}
//判断一个节点是否为红节点(即链接到此节点的链接颜色为红色)
bool is_red(Node * node) const
{
return (node) ? (node->color == RED) : false;
}
//取节点的所有孩子节点及其自身的节点数
size_t size(Node * node) const
{
return (node) ? (node->count) : 0;
}
//判断红黑树中是否存在指定的节点
bool contains(Node * node, const _Key & key)
{
while(node)
{
if (key < node->key) node = node->left;
else if (node->key < key) node = node->right;
else return true;
}
return false;
}
//取最小节点
Node * min(Node * node)
{
while(node && node->left) node = node->left;
return node;
}
//左旋转节点的右链接
Node * rotate_left(Node * node)
{
Node * p = node->right;
node->right = p->left;
p ->left = node;
p ->color = node->color;
node->color = RED;
//更新节点数量统计
p ->count = node->count;
node->count = size(node->left) + size(node->right) + 1;
return p;
}
//右旋转节点的左链接
Node * rotate_right(Node * node)
{
Node * p = node->left;
node->left = p->right;
p ->right = node;
p ->color = node->color;
node->color = RED;
//更新节点数量统计
p ->count = node->count;
node->count = size(node->left) + size(node->right) + 1;
return p;
}
//节点颜色转换(分解4-节点或向父节点'借'节点操作)
void flip_colors(Node * node)
{
node->color = (node->color == RED) ? BLACK : RED;
node->left->color = (node->left->color == RED) ? BLACK : RED;
node->right->color = (node->right->color == RED) ? BLACK : RED;
}
//插入新的节点
Node * put(Node * parent, const _Key & key, const _Value & value)
{
if(!parent) return new Node(key, value, RED);
if (key < parent->key) parent->left = put(parent->left, key, value);
else if (parent->key < key) parent->right = put(parent->right, key, value);
else parent->value = value;
/*左节点连接是黑色,右节点连接是红色,则左转节点
左倾红黑树不允许红色链接出现在右边,若有红色链接出现在右边就进行左旋转操作
('..'代表红色节点,'.'代表黑色节点)
3 5
.. => ..
.. ..
5 3
*/
if(!is_red(parent->left) && is_red(parent->right)) parent = rotate_left(parent);
/*
节点连接连续红色,右转节点
5
.. 3
.. ...
3 => .. ..
.. 1 5
..
1
*/
if(is_red(parent->left) && is_red(parent->left->left)) parent = rotate_right(parent);
/*
左右连接全为红色,则将左右连接设置为红色,其父节点设为红色
3 3
... => . .
.. .. . .
1 5 1 5
*/
if(is_red(parent->left) && is_red(parent->right)) flip_colors(parent);
//更新节点数量统计
parent->count = size(parent->left) + size(parent->right) + 1;
return parent;
}
//恢复左倾红黑树的平衡性
Node * balance(Node * node)
{
//'借孩子'操作可能导致红色节点出现在右边,这在左倾红黑树中是不可以出现的,需要左旋转进行修复
if(is_red(node->right)) node = rotate_left(node);
//左节点连接是黑色,右节点连接是红色,则左转节点
if(!is_red(node->left) && is_red(node->right)) node = rotate_left(node);
//左节点连接连续红色,右转节点
//is_red(node->left)若为红色节点则node->left必定存在
//所以此处is_red(node->left->left)是安全的
if(is_red(node->left) && is_red(node->left->left)) node = rotate_right(node);
//左右连接全为红色,则将左右连接设置为红色,其父节点设为红色
if(is_red(node->left) && is_red(node->right)) flip_colors(node);
node->count = size(node->left) + size(node->right) + 1;
return node;
}
//借一个红色节点给左孩子
Node * move_red_left(Node * node)
{
//首先向父节点借一个节点
flip_colors(node);
if(is_red(node->right->left))
{
//它的亲兄弟节点不是2-节点,从其亲兄弟借一个节点到左节点中
node->right = rotate_right(node->right);
node = rotate_left(node);
}
return node;
}
//移除最小的节点
Node * remove_min(Node * node)
{
if(node->left == nullptr)
{
delete node;
return nullptr;
}
/* 关于删除最小节点的规则
确保当前节点不是2-节点
1.如果当前节点的左节点不是2-节点,则继续
2.如果当前节点的左节点是-2节点,且它的亲兄弟节点不是2-节点,则从其亲兄弟借一个节点到左节点中
3.如果当前节点的左节点是-2,且它的亲兄弟也是2-节点,则将父节点中的最小键及其兄弟节点合并为一个4-节点 */
if(!is_red(node->left) && !is_red(node->left->left))
{
//非2-节点,父亲或亲兄弟节点借一个节点给左节点,以确保左节点不是2-节点
node = move_red_left(node);
}
node->left = remove_min(node->left);
//删除操作完成后需要由下至上分解所有4-节点
return balance(node);
}
//借一个节点给右孩子
Node * move_red_right(Node * node)
{
//同move_red_left的注释
flip_colors(node);
if(is_red(node->left->left))
{
node = rotate_right(node);
}
return node;
}
//移除最大的节点
Node * remove_max(Node * node)
{
/* 此处相较于删除最小节点多了一个步骤
若左孩子为红节点则进行右旋操作,让右节点成为红节点以便接下来的删除操作
根据左倾树的性质 若左孩子非红色节点,则必然存在有右子节点
假设此处不进行右旋,则下列例子的平衡将遭到破坏
2
.. 由于2节点的右孩子为空,所以2节点是最大节点,此时C1.0处的代码将直接
.. 删除2节点,其左节点也被被抛弃
1
*/
if(is_red(node->left)) node = rotate_right(node);
//C1.0
if(node->right == nullptr)
{
delete node;
return nullptr;
}
if(!is_red(node->right) && !is_red(node->right->left))
{
node = move_red_right(node);
}
node->right = remove_max(node->right);
//删除操作完成后需要由下至上进行恢复
return balance(node);
}
//将移除最小的节点和移除最大的节点实现结合在一起,即可实现删除任意节点
Node * remove(Node * node, const _Key & key)
{
if(key < node->key)
{
//和删除最小节点时的操作类似,判断节点的左孩子是否为2-节点,若非2-节点则需要借一个红色节点给左孩子
if(!is_red(node->left) && !is_red(node->left->left))
{
node = move_red_left(node);
}
node->left = remove(node->left, key);
}
else
{
if(is_red(node->left)) node = rotate_right(node);
if(node->key == key && (node->right == nullptr))
{
delete node;
return nullptr;
}
//和删除最大节点的操作类似
if(!is_red(node->right) && !is_red(node->right->left))
{
node = move_red_right(node);
}
if(node->key == key)
{
//找到node的后继节点
Node * minNode = min(node->right);
//将后继节点的key-value移动给node
node->key = std::move(minNode->key);
node->value = std::move(minNode->value);
//删除最小节点无需使用节点的key/value数据,只会不断向左直到最小的那个节点
node->right = remove_min(node->right);
}
else
{
node->right = remove(node->right, key);
}
}
//删除操作完成后需要由下至上进行恢复
return balance(node);
}
void print(Node * node) const
{
if(node == nullptr) return;
std::cout << ((node->color == RED) ? 'R' : 'B') << '(' << (node->key) << ')' << ' ';
print(node->left);
print(node->right);
std::cout << "BACK ";
}
public:
LLRBT() = default;
LLRBT(const LLRBT & rhs) = delete;
LLRBT(const LLRBT && rhs) = delete;
LLRBT & operator=(const LLRBT & rhs) = delete;
LLRBT & operator=(const LLRBT && rhs) = delete;
~LLRBT()
{
clear(root_);
}
void clear()
{
clear(root_);
root_ = nullptr;
}
size_t size() const
{
return root_ ? size(root_) : 0;
}
void put(const _Key & key, const _Value & value)
{
root_ = put(root_, key, value);
root_->color = BLACK;
}
_Value * get(const _Key & key) const
{
for(Node * node = root_; node != nullptr; )
{
if (node->key < key) node = node->right;
else if (key < node->key) node = node->left;
else return &(node->value);
}
return nullptr;
}
void remove_min()
{
if(root_ == nullptr) return;
if(!is_red(root_->left) && !is_red(root_->right))
{
root_->color = RED;
}
root_ = remove_min(root_);
if(root_) root_->color = BLACK;
}
void remove_max()
{
if(root_ == nullptr) return;
if(!is_red(root_->left) && !is_red(root_->right))
{
root_->color = RED;
}
root_ = remove_max(root_);
if(root_) root_->color = BLACK;
}
void remove(const _Key & key)
{
//判断树中是否存在这个key
if(!contains(root_, key)) return;
if(!is_red(root_->left) && !is_red(root_->right))
{
root_->color = RED;
}
root_ = remove(root_, key);
if(root_) root_->color = BLACK;
}
void print() const
{
print(root_);
std::cout << std::endl;
}
};
int main()
{
int testCount = 7;
int keys[] = {6, 7, 1, 5, 3, 4, 2};
LLRBT<int, int> st;
for(int i = 0; i < testCount; ++i)
{
std::cout << "put:" << keys[i] << std::endl;
st.put(keys[i], keys[i]);
//st.print();
}
for(int j = 1; j <= testCount; ++j)
{
st.remove(j);
std::cout << "\nremove:" << j << "\nsize:" << st.size() << std::endl;
for(int i = 1; i <= testCount; ++i)
{
int * p = st.get(i);
std::cout << (p ? *p : 0) << ' ';
}
std::cout << std::endl;
st.print();
std::cout << std::endl;
}
std::cout << std::endl;
std::cin.get();
return 0;
}